Carl Friedrich Gauss Kimdir? Gauss’un Hayatı ve Eserleri

Bilime, diferansiyel geometri, analiz, sayılar kuramı, manyetizma, jeodezi, optik ve astronomi alanlarına katkıda bulunmuÅŸ, antik çaÄŸlardan beri yaÅŸamış en büyük matematikçi ve matematikçilerin prensi olarak tanınan Johann Carl Friedrich Gauss, Roma Cermen Ä°mparatorluÄŸu’na baÄŸlı Braunschweig-Lüneburg Dükalığı’ndaki Braunschweig kentinde, 30 Nisan 1777’de Gebhard ile Dorothea Gauss çiftinin tek çocuÄŸu olarak dünyaya gelir.

Babası az eÄŸitimli bir taÅŸ ve duvar ustasıydı, annesinin ise okuma-yazması bile yoktu. Efsaneye göre, Gauss henüz üç yaşındayken, babasının kağıt üzerinde yaptığı hesapları kafadan kontrol edip düzelterek dehasını belli eder. Çocukluk yıllarında Gauss’un dehasını gösteren çok sayıda olay yaÅŸanır. Bu özelliÄŸine iliÅŸkin birçok hikaye mevcut olsa da, bunlardan en meÅŸhur olanı şöyledir: Gauss’un ilkokul öğretmeni J.G. Büttner, öğrencilerinden 1’den 100’e kadar olan sayıları toplamalarını isteyince, küçük Gauss cevabı birkaç saniye içinde bularak öğretmenini büyük bir ÅŸaÅŸkınlığa uÄŸratır. Gauss, sayı listesinin iki zıt ucundan birer sayı alıp topladığında hep aynı sonucu elde ettiÄŸini görür (1+100 = 101, 2+99 = 101, 3+98 = 101, 4+97 = 101 vb.) ve böyle devam edip gider. Toplam 50 tane 101 eder, o zaman yanıt 5050 olmalıdır.

Christian Albrecht Jensen, Carl Friedrich Gauss, 1850

Yoksul bir ailenin çocuÄŸu olan Gauss, Braunschweig Dükü Karl Wilhelm Ferdinand’ın verdiÄŸi burs sayesinde, 1792’den 1795’e kadar Collegium Carolinum’da (Braunschweig Teknik Ãœniversitesi) öğrenim görür. 1795’te Göttingen Ãœniversitesi’ne kayıt olduÄŸu sırada, matematikçi mi yoksa yazar mı olmak istediÄŸine henüz karar verememiÅŸtir, kararsızlığı altı ay kadar sürer. Sonunda 30 Mart 1796 tarihinde günlüğüne “Bugün eÅŸkenar bir onyedigenin cetvel ve pergelle nasıl çizileceÄŸini buldum” yazar. Kenar sayısı bir Fermat asalı olan her düzgün çokgenin, sadece pergel ve cetvel yardımıyla çizilebileceÄŸini ispatlar. Antik Yunan’dan beri matematikçileri meÅŸgul eden bu problemin çözümü, aynı zamanda Gauss’u matematikçi olmaya da ikna eder. Gauss bu baÅŸarısından o kadar memnun olur ki, mezar taşına bir düzgün onyedigenin oyulmasını vasiyet eder. Ancak daireye çok yakın olan bu ÅŸeklin oyulması çok zor olacağından, vasiyetini yerine getirecek bir taÅŸ ustası bulamaz.

1796 Gauss için oldukça verimli bir yıl olur. Düzgün çokgenlerle ilgili keÅŸfinden bir ay kadar sonra, yine kendi keÅŸfi olan modüler aritmetik fikrini kullanarak, sayılar kuramında karesel karşılıklılık ilkesi olarak bilinen çok önemli teoremi kanıtlar. Ä°lk olarak Euler ve Legendre tarafından ortaya atılmış, ama kanıtlanamamış olan bu teorem, ikinci dereceden denklemlerin çözülebilirliÄŸinin belirlenmesini saÄŸlar. Yine aynı yıl içinde Gauss, asal sayıların tamsayılar arasındaki dağılımına iliÅŸkin önemli bir sonuç bulur. Bundan kısa bir süre sonra da, her tamsayının en fazla üç üçgensel sayının toplamı olarak yazılabileceÄŸini kanıtlar ve 10 Temmuz 1796’da günlüğüne ÅŸu notu düşer: “Eureka! Num = â–²+â–²+â–².” Ekim 1796’da ise katsayıları sonlu bir cisimden gelen polinomların çözümleriyle ilgili bir sonuç yayımlar. (Bu sonuç, 150 yıl sonraki Weil varsayımlarının da çıkış noktası olur.)

22 yaşındayken cebirin temel teoreminin (D’Alembert Gauss Teoremi) ilk ispatını vererek doktorasını alan Gauss, sonraki yıllarda teoremin üç ispatını daha yapar.

1801 yılında bir Ä°talyan astronom Mars ve Jüpiter arasında bir gezegen bulduÄŸunu açıklar. DiÄŸer astronomlar da bu iddiayı kanıtlamak için yarışırlar. Ancak bilim adamları, gezegenin yerini saptamak konusunda baÅŸarılı olamaz.  Bu gezegenciÄŸin bulunmasıyla Gauss astronomiye ilgi duymaya baÅŸlar. Gauss, En Küçük Kareler Metodu’nu yeni gezegenle ilgili gözlemlere uygulayarak, nerede görülebileceÄŸini belirler. Bundan birkaç ay sonra astronomlar, Gauss’un öngördüğü yere teleskoplarını yönlendirdiler ve gerçekten de gezegeni bulurlar. Astronomlar bu gezegene Ceres adını verirler. Ceres, günümüzde Mars ile Jüpiter arasındaki yörüngede bulunan binlerce kaya parçası içindeki ilk küçük gezegen ya da asteroittir. Gauss’un bu buluÅŸu, uluslararası alanda tanınmasına yol açar. Bu sırada, sadece 24 yaşındadır.

Regresyon analizi (iki ya da daha çok deÄŸiÅŸken arasındaki iliÅŸkiyi ölçmek için kullanılan analiz metodu) yaparken en çok kullanılan yöntemlerden biri olan En Küçük Kareler Yöntemi’ni, Gauss 18 yaşındayken geliÅŸtirir. Zaten pek çok matematiksel keÅŸfini henüz 20 yaşına gelmeden yapar. Bu yöntemi, ilk kez 1801’de Ceres astroidinin yörüngesinin belirlenmesinde kullanır ve Gauss’un toplu eserlerinin yayınlandığı ciltlerden ikincisinde 1809 yılında yayınlanır. Fransız matematikçi A. Legendre 1805 ve Amerikalı matematikçi R. Adrain da 1808 yıllarında aynı yöntemi Gauss’dan habersiz ve bağımsız olarak keÅŸfederler. En küçük kareler yöntemi, tıp, finans, mühendislik, ziraat, biyoloji ve sosyoloji gibi çeÅŸitli bilim dallarında çeÅŸitli deÄŸiÅŸkenler arasındaki iliÅŸkiler belirlenirken kullanılan en önemli araçlar arasındadır.

Gauss’un ikinci eseri, 1802 yılında bulunan diÄŸer bir gezegencik olan Pallas’ın hareketleriyle ilgilidir.

Kendisine ün kazandıran geliÅŸmeden birkaç ay sonra büyük eserini yayınlar. Sayılar kuramının önemli sonuçlarını derleyip kendi katkılarını da ekleyerek yazdığı Disquistiones Aritmeticae’yı (Aritmetik AraÅŸtırmaları), 21 yaşında (1798) bitirmiÅŸse de, kitap olarak 1801’de basılır. Kitabında Euler, Fermat, Lagrange gibi kendinden önceki büyük matematikçilerin çalışmalarını toparlayarak kendi düşüncelerini de ekler. Gauss yöntem olarak önce teorem, sonra kanıt ve en son olarak teoremin sonuçları sıralamasını kullanır. Matematikte bir klasik olan Aritmetik AraÅŸtırmaları’nda deÄŸindiÄŸi çok sayıda önemli konuyu, daha sonra ayrıntılı bir ÅŸekilde inceleyerek adeta olgunlaÅŸtırır. Gauss, matematiÄŸi bilimlerin kraliçesi, sayılar teorisini de matematiÄŸin kraliçesi ilan eder.

Eseri okuyan Lagrange ise Gauss’a ÅŸunları yazar: “Eseriniz sizi bir anda birinci sınıf matematikçiler arasına yükseltmiÅŸtir. Uzun zamandan beri yapılmış en güzel analitik keÅŸfi ihtiva eden son bölümü, çok önemli kabul ediyorum.”

Disquisitiones arithmeticae

Gauss, ilk evliliğini 1805 yılında Johanna Osthoff ile yapar. Bu evlilikten Joseph adında bir oğlu ve Wilhelmine adında bir kızı olur.

“Kalbimdeki tutkuyu bu sanatsız ama dobra sözlerle size sundum deÄŸerli insan. Bunu bambaÅŸka türlü de yapabilirdim. Cazibenizin resmini çizebilirdim, ki bu tamamen gerçekleri yansıtsa da siz bunu iltifat olarak kabul ederdiniz; tutuÅŸan renklerle size olan aÅŸkımın resmini çizebilirdim ve elbette bunun için sadece kalbimi dinlemek yeterli olacaktı. Siz arzularımı kabul veya reddettikten sonra beni bekleyen mutluluÄŸu veya üzüntüyü tarif edebilirdim. Ama bunu yapmak istemedim. Bu yüzden benim bu bencil olmayan aÅŸkımın saflığından kuÅŸku duymayın. Kararınızı etkilemek istemiyorum. Hayatınızın bu en önemli meselesinde, dışardan düşüncelerin sizi etkilemesine izin vermeyin. Benim mutluluÄŸum için kendinizi feda etmemelisiniz. Kararınıza yön verecek olan sizin kendi mutluluÄŸunuz olmalı. Evet dünyanın en deÄŸerli varlığı sizi o kadar çok seviyorum ki, ancak benim olmanız beni mutlu edebilir, eÄŸer siz de isterseniz elbet. En sevgili, kalbimin ta içini size açtım; kararınızı heyecan ve korkuyla bekliyorum. Tüm kalbimle.” (Gauss’un Johanna Osthoff ‘a yazdığı 12 Temmuz 1804 tarihli mektubu) 

Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientium

Gauss’un hayatında çalkantılı bir dönem baÅŸlar. Önce kendisine burs ve destek veren Braunschweig Dükü, Prusya ile girilen savaÅŸta öldürülür. 1808 yılında babasını, 1809’da Louis adını verdikleri üçüncü çocuÄŸun doÄŸumu sırasında eÅŸi Johanna’yı kaybeder. Louis de henüz bir yaşına gelmeden ölür. Gauss, bu ölümlerden dolayı girdiÄŸi depresyondan asla tam anlamıyla kurtulamaz. Ancak tüm bu acılara raÄŸmen Gauss bilimsel çalışmalarını aksatmaz. 1809’da gök cisimlerinin hareketleri ile ilgili iki ciltlik eseri Theoria motus corporum coelestium in sectionibus conicis solem ambientium (GüneÅŸ çevresinde konik kesitler üzerinde hareket eden gök cisimlerinin hareketlerinin teorisi) adlı eserini yayımlar. Bu eser, günümüz bilimlerinde yaygın olarak kullanılan en küçük kareler yöntemini de ayrıntılı olarak ele alır. Eserin birinci cildinde diferansiyel denklemler ve eliptik yörüngeler hakkında bilgi verirken, ikinci cildinde gök cisimlerinin yörüngelerinin hesaplanmasıyla ilgili bilgiler verir.

1810’da karısının arkadaşı Minna Waldeck ile evlenir. Bu evlilikten de üç çocuÄŸu dünyaya gelir: Eugene, Wilhelm, Therese.

Gauss, diğer matematikçilerden farklı olarak, salt matematikten ilgi alanına giren konulara yönelik çalışmalara kadar, çok farklı alanlarda kilit buluşlara imza atar. Yapıtlarıyla matematik dünyasına yeni bir soluk getirdiği için bilim çevresinde Matematiğin Prensi olarak adlandırılır.

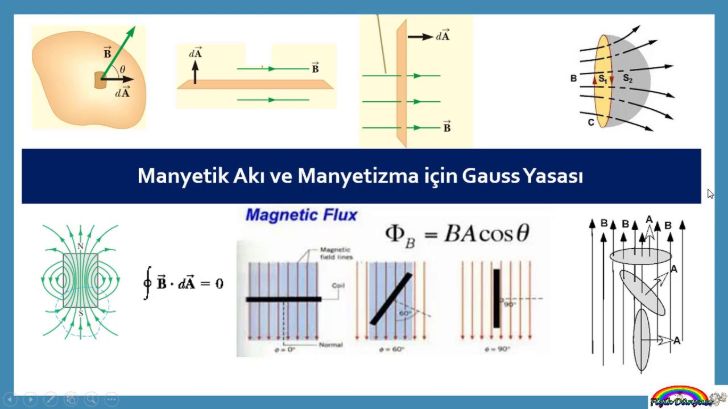
1830’lu yıllarda Gauss, Alman fizikçi Wilhelm Weber ile bir ekip kurup, o günlerde büyük bir karmaÅŸa yaratan elektromanyetizma teorisini yeniden ele alır. 1832 yılında manyetik olayların ölçülmesini olanaklı kılan sistemi geliÅŸtirir. Ayrıca, elektromanyetik yüklerin etkileri hakkında çok önemli teoremlere ulaşır. 1833 yılında manyetik kuvvetlerle ilgili yazdığı bir makalede manyetizmanın üç temel ölçümünü belirtir: Kütle, uzunluk ve zaman. Dünyanın manyetik alanıyla ilgili önemli çalışmalar yapar.

1831 yılında Ä°ngiliz kaptan James Clark Ross, manyetik kuzey kutbunun Gauss’un hesaplayarak bulduÄŸu bölgeye çok yakın bir yerde olduÄŸunu tespit eder. Benzer ÅŸekilde 1841 yılında da Amerikalı Kaptan Charles Wilkes, manyetik güney kutbunun Gauss’un hesaplama ile bulduÄŸu yere çok yakın bir yerde olduÄŸunu tespit eder. Uzun yıllar boyunca standart manyetik kuvvet birimi Gauss olarak kabul edilir. Bugün de manyetik alan birimi olarak, CGS’de (santimetre (uzunluk), gram (kütle) ve saniyeden (zaman) oluÅŸan birim sistemi) Gauss, MKS’de (metre (uzunluk), kilogram (kütle), saniyeden (zaman) oluÅŸan birim sistemi) ve SI birim sisteminde (uluslararası birim sistemi) Tesla kullanılır (1 Tesla = 10.000 Gauss).

Gauss, istatistik bilimine de önemli katkılar yapar. 17. yüzyılda William Petty ve John Gaunt’un Londra’da hazırladığı ölüm vakalarıyla ilgili cetveller, istatistik biliminin ilk temel taşları sayılabilir. Toplanan verilerin daha sistematik incelenmesi, matematiksel istatistiğin doğmasını sağlar. Belçikalı Lambert Quetelet, topladığı verileri inceleyerek daha önce Fransız matematikçi Abraham de Moivre tarafından ortaya atılan normal dağılımın kullanım alanını genişletir.

Gauss, Hannover’de yaptığı yüzey ölçümleri sırasında, ölçüm hatalarının istatistiksel dağılımını veren (daha önce astronomi araÅŸtırmalarında da kullandığı) normal dağılım fikrini kafasında iyice belirginleÅŸtirir. Ayrıca bu ölçümler Gauss’un diferansiyel geometriye de (eÄŸriler ve yüzeylerle ilgilenen bir matematik dalı) ilgi duymasını saÄŸlar. Bugün normal dağılım, Gauss dağılımı ya da kabaca çan eÄŸrisi diye de tanımlanır. Gauss dağılımı, ya da normal dağılım, bir ortalama deÄŸer etrafında toplanmış rastgele sayıların bir modelidir. Bazı doÄŸal süreçleri iyi modellediÄŸi söylenir. ÖrneÄŸin, bir hedefe niÅŸan alarak ok atarsanız, niÅŸan aldığınız yer ile vurduÄŸunuz yer arasındaki mesafe normal dağılımlı bir rastgele sayı olarak modellenebilir.

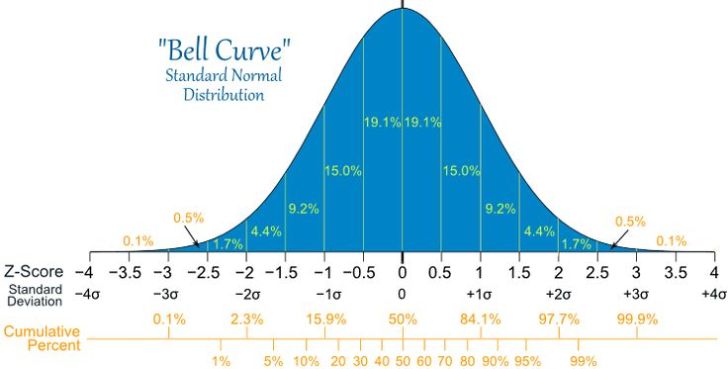
Matematiksel deÄŸerlerin incelenmesine yarayan ünlü çan eÄŸrisi, ilk kez Fransız matematikçi Abraham de Moivre tarafından 1733’te keÅŸfedilmekle birlikte, Gauss tarafından yeniden tanımlanır ve deÄŸerlendirmelerde kullanılan matematiksel iÅŸlemler, onun tarafından gerçekleÅŸtirilir. Gauss, geliÅŸigüzel etmenler nedeniyle bir yayılma söz konusuysa, eÄŸrinin belirgin bir ÅŸeklinin olması gerektiÄŸini belirtir. Zaten, bunun için bir formül de geliÅŸtirip ve eÄŸriye çan ÅŸeklini uygun görür. Bu eÄŸri her alana uygulanmaz. Ancak, iki sayı arasında doÄŸru çizilmeye olanak tanıyan birçok olgunun açıklanmasında iÅŸe yarar. Bu durumda, ortalama deÄŸer, çan eÄŸrisinin doruk noktasını oluÅŸturur. Standart sapma da eÄŸrinin diÄŸer tarafa geçiÅŸ eÄŸilimini sergiler. Bu iki sayı arasındaki bağıntı yüzde oranını verir. ÖrneÄŸin, bir sınıfta çoÄŸu öğrenci ortalama bir not aldıysa, yüksek ve düşük not alan kiÅŸi sayısı azsa, sınıftaki not dağılımı normal dağılımla (çan eÄŸrisiyle) gösterilebilir. Çan eÄŸrisinin iki kolunun arasının ne kadar dar ya da geniÅŸ olduÄŸunu standart sapma (sigma) deÄŸeri belirler. Sigma küçükse eÄŸri dardır, büyükse geniÅŸtir.

 Gauss’un 17 yaşındaki imzası

Gauss, geometrik ÅŸekillerin veya üç boyutlu cisimlerin bazı durumlarda deÄŸiÅŸmeyen özelliklerini inceleyen matematik dalı olan topoloji üstünde yoÄŸunlaşır. Topoloji, bükülen, eÄŸrilen cisimleri inceler. Topolojiye bazen lastik levha geometrisi de denir. Gauss, manyetizma üzerine yaptığı çalışmalarda, günümüzde geçiÅŸme sayısı olarak bilinen bir topolojik deÄŸiÅŸmez gösterir. Bu sayı, kapalı bir eÄŸrinin bir baÅŸkasının üzerine nasıl sarıldığını belirler. Gauss, topoloji hakkında bir önseziye sahipti ve bu dalın evreni kavramakta çok önemli bir yere sahip olduÄŸunu düşünür. Tarih, bu konuda da Gauss’u haklı çıkarır, çünkü topoloji, bugün teorik fiziÄŸin kalbini oluÅŸturur. Evrendeki parçacıkların özellikleri ve aralarındaki güç iliÅŸkisi, topolojinin yardımıyla açıklanır. Ancak topolojinin geliÅŸmesi Gauss’un öğrencisi olan Johann Listing ve asistanı Augustus Möbius sayesinde olacaktır.

Gauss, jeodeziyle yani yeryüzünün boyutlarını ve biçimini konu olarak inceleyen bilim dalıyla ilgili 1799 yılında bazı çalışmalar yapsa da, gerçek anlamda jeodezi çalışmalarına 1818 yılında baÅŸlar. Arazi ölçümleri sırasında ışıkla iÅŸaret verebilmek için helyotrop cihazını geliÅŸtirir. Helyotrop, güneÅŸ ışığını istenilen yöne yansıtmak için döndürülebilen bir cihazdır. Böylece aralarında onlarca kilometre bulunan kiÅŸilerin birbirlerinin yerlerini tespit etmeleri saÄŸlanarak gerekli mesafe ve açı ölçümleri yapılabilir. Gauss, yerkürenin È™eklini “Yeryuvarının geometrik anlamdaki yüzeyi denilen ÅŸey, öyle bir yüzeydir ki, gravite  vektörü doÄŸrultusunu her yerde dik keser ve tüm deniz yüzeyi bundan bir parçadır” şeklinde tanımlar.

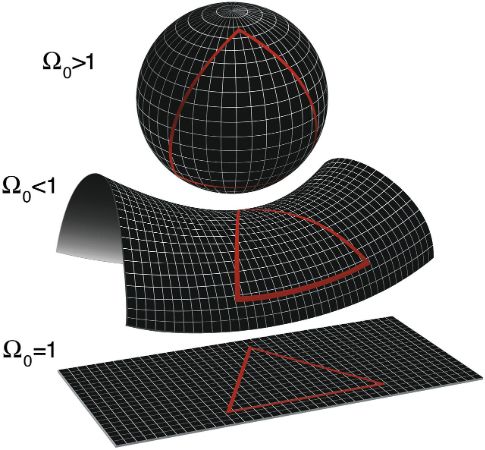
Yüzey eÄŸriliÄŸi ile ilgili araÅŸtırmalar, Antik Yunan’dan baÅŸlayarak, Descartes, Kepler, Fermat ve Huygens’in çalışmalarının ardından 17. yüzyılda Newton ve Leibniz tarafından Kalkülüs’ün geliÅŸtirilmesi ile hız kazanır. Bu geliÅŸmelerden türeyen eÄŸrilik fikri, Öklit geometrisinin önermelerini yeniden sorgulamaya, uzay, zaman ve yer çekiminin matematik ve fizik anlamının netleÅŸtirilmesine yol açarak bu bilim alanlarında önemli geliÅŸmelere neden olmuÅŸtur. Günümüzde eÄŸrilerin ve yüzeylerin eÄŸriliÄŸi diferansiyel geometrinin konularıdır.  1828 yılında Gauss, muhteÅŸem teoremi Theorema Egregium‘da, yüzeyin eÄŸriliÄŸini ölçmede, bugün Gauss eÄŸriliÄŸi adı verilen bir ölçümün olduÄŸunu ortaya koyar ve bu ölçümün sadece yüzey üzerindeki eÄŸrilere baÄŸlı olduÄŸunu gösterir. Bu ölçü, yüzeyin ÅŸeklinin deÄŸiÅŸmesi ile deÄŸiÅŸmez. Gauss’un bu keÅŸfi bugün içsel geometri olarak adlandırılır. Yani yüzey üzerinde yaÅŸayan bir canlı, bu ölçüyü (Gauss eÄŸriliÄŸi) kullanarak yüzeyin eÄŸriliÄŸi hakkında bilgi edinebilir. Bu eÄŸrilik tanımı, cisimlerin içinde bulundukları uzaydan bağımsız, içkin olarak sahip oldukları eÄŸriliktir.

C. F. Gauss, Braunschweig

Gauss, kendisini örnek alan genç matematikçileri desteklemediÄŸi için çok eleÅŸtirilir. Pek çok meslekdaşı onu mesafeli ve katı bulur. Gauss, öğretmenlikten nefret ettiÄŸini söylese de, Richard Dedekind, Bernhard Riemann, Friedrich Bessel gibi bazı öğrencileri sonradan baÅŸarılı matematikçiler olurlar. Gauss’un babasıyla arası iyi deÄŸildir, zira Gauss’un okumasını istemez, kendisi gibi taÅŸ ustası olmasını ister. Gauss, eÄŸitimi boyunca babasından görmediÄŸi desteÄŸi annesinden görür. Ne garip bir çeliÅŸkidir ki, Gauss da oÄŸullarıyla iyi geçinemez, oÄŸlu Eugene’nin ve daha sonra Wilhelm’in ABD’ye göç etmesine sebep olur.

Gauss, 1807’de astronomi bölümüne profesör olduÄŸu Göttingen Ãœniversitesi’nde ömrünün sonuna kadar kalır. Son yıllarında edebiyatla ilgilenir. Gauss, 23 Åžubat 1855’te 78 yaşında Göttingen’de ölür. Beyni araÅŸtırma için muhafaza edilir ve bugün hala Göttingen Ãœniversitesi’nin Tıp Fakültesi’nde formalin içinde korunur.

• Gauss’un resmi 1989 – 2001 yılları arasında, bir normal dağılım eÄŸrisiyle beraber, 10 DM banknotlarının üzerine basılır.
• Almanya’nın Dransfeld kentindeki 51 metrelik beton gözlem kulesinin adı Gauss Kulesi’dir.
• CGS sistemindeki manyetik alan birimi 1 Gauss’tur. Gauss’un ismi matematik ve fizikte pek çok teorem, formül ve kavrama verilir.
• 1977’de Gauss’un doÄŸumunun 200. yıldönümünde, DoÄŸu Almanya ve Batı Almanya’da ayrı ayrı hatıra pulları basılır.
• Ay’daki Gauss krateri, 1001 Gaussia asteroidi ve Antarktika’da sönmüş bir volkan olan Gaussberg, Gauss’un anısına isimlendirilir.
• 2005 yılı, Gauss’un 150. ölüm yıldönümü olması nedeniyle Gauss yılı ilan edilir.

Kaynak
Carl Friedrich Gauss, Matematikçiler Prensi: Carl Friedrich Gauss, Carl Friedrich Gauss: Rakamlarla Oynamak, En Küçük Kareler Yöntemi, Gauss’un Evlenme Teklifi, Riemann’ın manifold kavramı ve yeni bir mekân-geometri inşasındaki yeri, Mimarlıkta Yüzey Panelleme Yaklaşımlarının Gauss Eğriliği İle İlişkisi